Datavu: Binomial distribution : Concepts and problems from Brandon Foltz video

Binomial experiment has following characteristics:

The process consists of sequence of n trials.

Only two exclusive outcomes are possible in each trial. One outcome is called success and other is called failure.

The probability of success is denoted by p and it does not change from trial to trial. It means probability of failure is (1 - p) and that is also fixed for trial to trial.

The trials are independent and outcome of any trial do not influence future trials.

Some common notations,

n: Number of trials

x: Number of successes

P: Probability of success

Lets visualize couple of scenarios,

In the screenshot above first example is of,

n = 5

x = 2

the second example is of,

n = 5

x = 4

Ofcourse there are other ways then shown in screenshot above for given values of x and n.

Lets try to understand all possible ways in which this can happen for,

n = 5

x = 4

Now lets take one example and try to solve it.

Problem 1: A (very poor) manufacturer is making a product with 20% defect rate. If we select 5 randomly chosen items at the end of assembly line, what is the probability of finding one defective item in our sample.

So lets enlist all the ways in which (exactly) 1 product can be defective.

Now lets convert this into probability based table,

In the screenshot above we can see the general formula, where

n: Number of trials

x: Number of successes

P: Probability of success

So based on this formula we can calculate all number of successes immediately:

Lets have one more example,

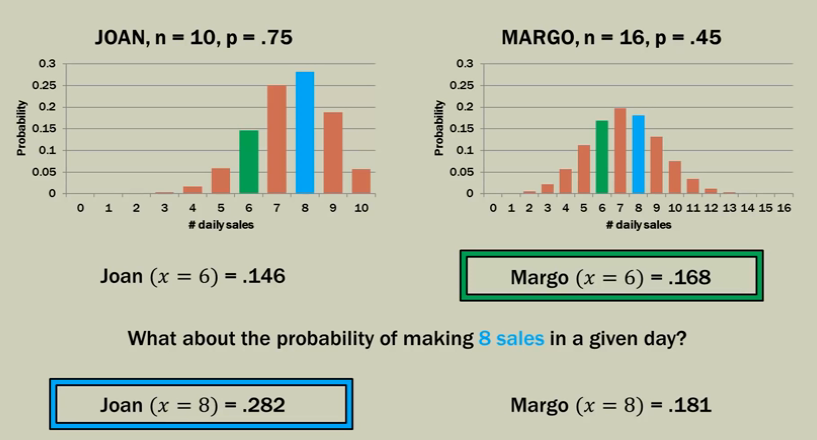
As a sales manager you analyze the sales records for all salespersons under your guidance. Joan has success rate of 75% and averages 10 sales call per day. Margo has a success rate of 45% and averages 16 calls per day. What is the probability of each sales person making 6 sales on any given day.

Using the formula we have,